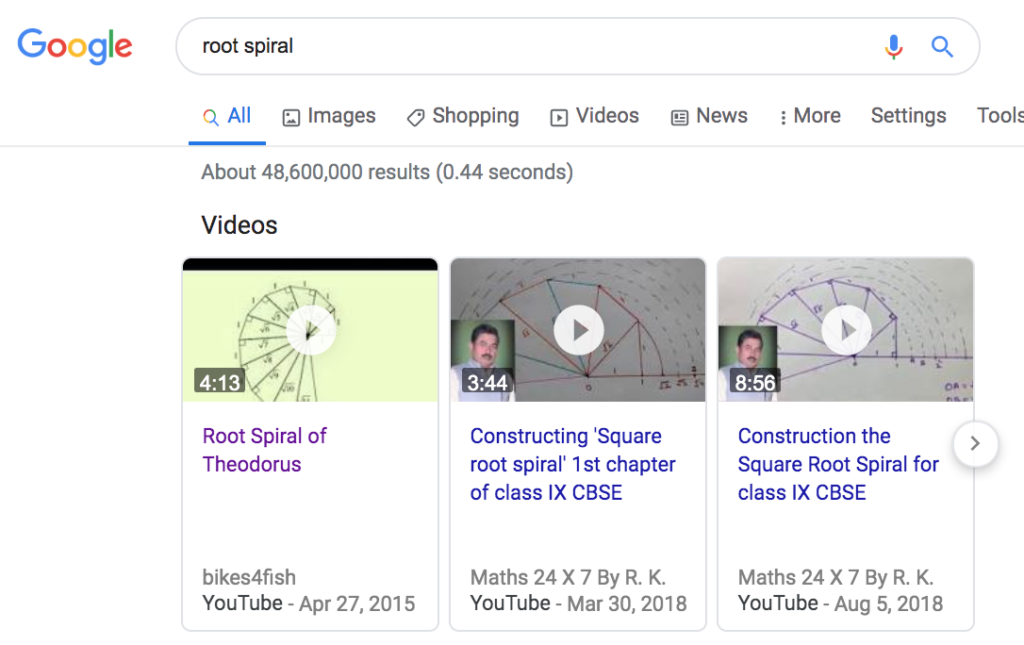
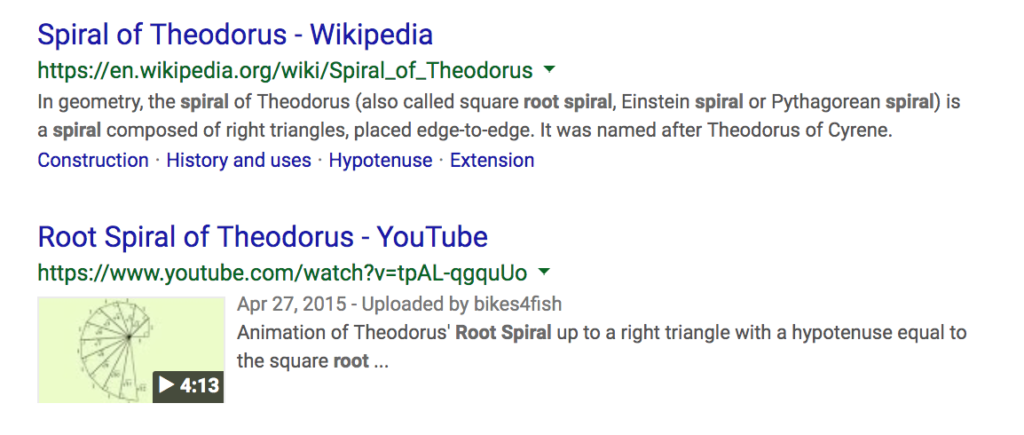
I saw this on X (formerly known as Twitter) and thought it was both intriguing and appalling in a variety of ways. Please have a look for yourselves and take stock of the situation before you start trying to answer the question at the end: what would you do now?
<deep breath>
The 3rd grade teacher (and her principal) should know that division comes from multiplication. If some number A times some other number B gives us a result, which we’ll call a product, then the product divided by the number A will give us the number B, and/or the product divided by B will equal A.
As H-H Wu puts it in his essential text, Understanding Numbers in Elementary School Mathematics (p. 97), “Division is an alternate, but equivalent, way of expressing multiplication.”
When we divide 24 by 3 and get an answer, it means that 3 times our answer (if it’s a correct answer) will give us 24. In other words, for the division to be do-able, 24 has to be a multiple of 3. The number we’re dividing up has to be a multiple of the divisor. This is the way students—or anyone—can check to see if their quotient is correct.
But 1 is not a multiple of 0. The 3rd grade teacher and principal’s claim is that 1 ÷ 0 = 0 is equivalent to saying that 0 × 0 = 1. This obviously false statement goes deeper, I think, than just being a wrong answer; it suggests that the 3rd grade teacher and her principal don’t get the relationship between multiplication and division—a crucially important understanding for students to arrive at, since it’s part of the essential foundation for math in middle school, high school, and beyond.
But back to 1 ÷ 0. The division can’t be done since there is no number you can multiply by 0 and get 1. Likewise for any other nonzero number divided by 0. Whatever number you get for a result, when you multiply it by 0, you’ll just get 0. So division by 0 can’t be done, since whatever multiplication it relies on will be false: zero times any number equals zero.
It’s great to see principals backing up their teachers, but both the teacher and her principal should have checked their work. The argument over right vs. wrong should have been over whether 0 times 0—or 0 times any number—will equal 1.
To wind this up, where do I think the errors lay? <begin speculation>
- Misunderstanding that division entails multiplication: If two numbers are multiplied and give you a product, the product divided by either of the numbers will give you the other number. This is why division by zero cannot be done, or, as put more elegantly but I think more confusingly (at least to most 3rd graders and many of their teachers) “Division by zero is undefined.”
- Failure to check their division with multiplication, which has the effect of providing no reasoning to back up their (erroneous) claim.
- Where did the answer of 0 come from? Who knows for sure—but I suspect, from having talked about arithmetic with K-8 students, mostly remedial students, for most of my teaching career, I recall some students treated 0 as meaning something like “can’t do it, impossible”.
- The 3rd grade teacher and her principal could have gotten the symbols shuffled somehow. It is true that 0 ÷ 1 = 0 since 1 × 0 = 0. But division is not commutative; shufflng usually leads to an error.
- The weirdness of 0. The idea of having a number standing for nothing is and has been a mind-blower for humans, young and old throughout human history, so we should be at least somewhat charitable towards the 3rd grade teacher and her principal.
Offering an answer to the parent’s what-should-I-do question, I would suggest that the parent should get to the heart of the multiplication-division relationship and ask teacher and principal to check their work, testing whether multiplying divisor (0) and quotient (0) gives them a product equal to the dividend (1).
Enough for now. Remember to support your claims by checking your work!