Here are some things—slideshows and pdfs—I’ve found handy for helping kids get the picture of single-digit multiplication. And here’s one for teachers and parents, Picturing Multiplication, to give you an overview of what I have in mind.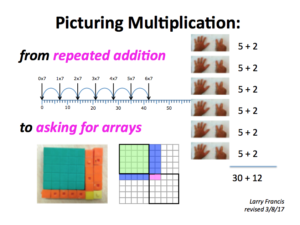
Download and enjoy!
Some PowerPoints that combine the concepts of number-as-length and decomposing into addends that make tens may help students get a picture of and a handle on their single-digit facts the sequence of 3’s (nx3), the sequence of 4’s (nx4), the sequence of 6’s (nx6), the sequence of 7’s (nx7), and the sequence of 8’s (nx8). You can download a little (4.25″ x 5.5″) 14-page booklet for recording these sequences in either pdf or docx format.
I’ve included a pdf, Multiplication, a story of 7’s, that transcribes a talked-through sequence of 7 after 7, decomposing each additional 7 into addends that make a new 10 with the previous total (when possible). The addend not used to make a fresh 10 is the overlap that goes beyond the new 10 as the new amount of ones. This would be an exceedingly tedious thing to have to do very often, but it’s a good thing to be able to do. (This activity makes a good companion or foll0w-up to the PowerPoints shown above.)
Multiplication facts on a 10×10 grid (pptx) provides an overview that should make the task of memorizing 100 multiplication facts seem a lot more do-able by highlighting the easy columns and rows. A blank grid (pdf) for students to fill out and maybe color independently makes a good companion piece. There are two more grids, 0x0…10×10, one showing just the factors and another showing just the products.
A 0…120 grid (pdf—4 to a page) is a good way for students to record multiples and skip counting—and a good prop for them to discuss the patterns that emerge on the grid as they highlight the sequence(s). It could even be used to mark primes and composites. Here’s a pdf with a single 0…120 grid for those times when you want to be living large.
Having students build rectangular arrays sounds like a good idea in theory: they build 6×7 as 6 rows of 7 units each, for example. But in practice, it’s a royal pain for everyone: the teeny unit cubes or “ones” squirrel around and are very hard to keep in place, especially in the larger arrays (try having 81 of them!). Showing students how to use 5×1=5 or 1×5=5 lengths and 5×5=25 blocks is a good intro to partial products and makes for a neater, less frustrating activity, easier for everyone to manage. With 5×1 and 5×5 pieces, students never have more than 16 ones: they build their arrays with ones, fives, and 5×5 blocks, record the partial products, and the total. A page of 5×5 grids (pdf—4 to a page) is a good way for students to record their work with these arrays—with or without blocks. A little (4.25″ x 5.5″) 14-page booklet of 5×5 grids, pdf so you can print it right out or docx so you can modify it yourself, might be even better!