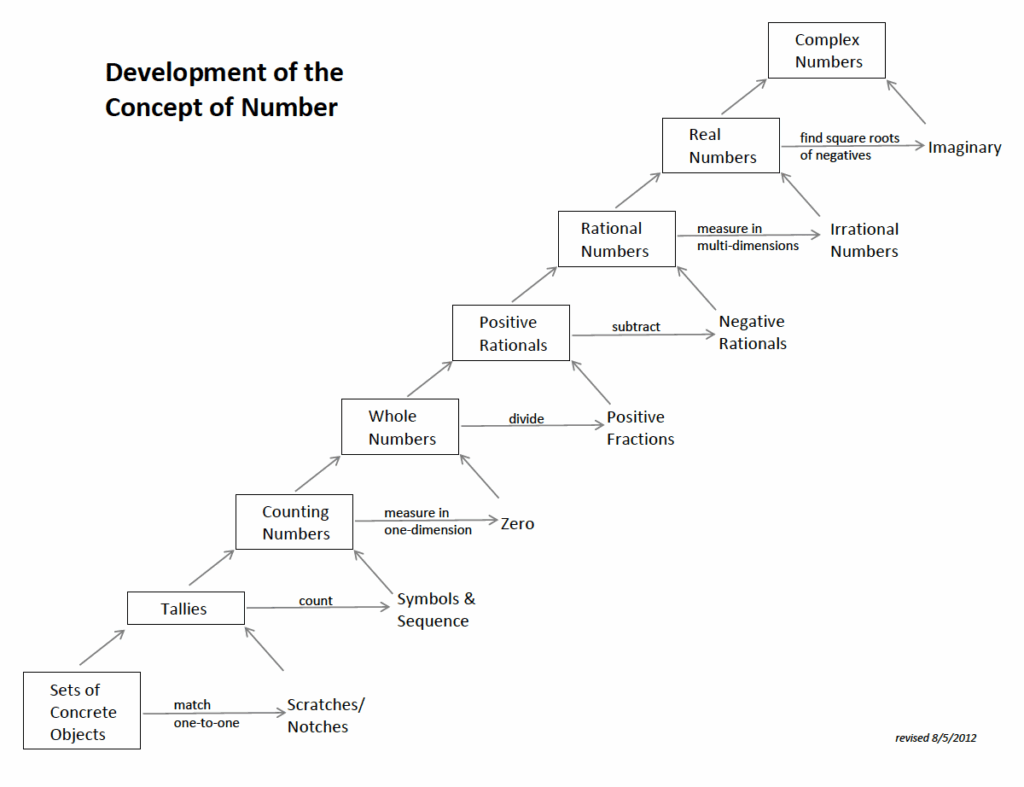
Adding fractions with unlike denominators has been a stumbling block for generations of students, their parents, and even their teachers. Many come up with 2/5 as their (spoiler alert: wrong!) answer since the numerators add to 2 and the denominators add to 5. Getting this fundamental calculation right—and knowing why it’s right—deserves an explanation that goes deeper than repeating an algorithm or memorizing a jingle. But I wanted to make the explanation simple and schematic enough to be generally accessible. Since the number line is the simplest schema for a concrete understanding of number (e.g., rulers, yardsticks, tape measures, etc. as well as the Common Core Math Standards 3rd grade). And since 1/2 and 1/3 are the simplest fractions I could think of, I picked them and made an animated slideshow (that needs PowerPoint) and a short video overview (that doesn’t).
The mp4 video is quite short, just 42 seconds. It provides a schematic overview of what’s going on conceptually when you add 1/2 and 1/3 on the number line and, I hope, a good intro to what the PowerPoint slideshow covers in more detail, both on the number line and symbolically. (click the triangle to play the video)
The PowerPoint is longer, but it provides a more complete explanation and gives teachers the basics of what they would need to extend the addition of 1/2 and 1/3 to the addition of any two fractions with unlike denominators (since the commutative property of multiplication can be depended on with all nonzero whole numbers, whether 2•3=3•2 or a•b=b•a. Keep in mind that PowerPoint is a proprietary Microsoft program: you may need to download it from your browser and then open it in PowerPoint. (The extensive animations will not play properly without PowerPoint.)
I didn’t include a narration with these presentations because I think my voice (especially my chronic stuttering) would be a distraction. I tried to make the text be a good enough explanation on its own, but I encourage you to add your own voice and/or get your students to add theirs.
These presentations are based on my reading of Wu’s Understanding Numbers in Elementary School Mathematics, Chapter 14, “Addition of Fractions and Decimals”, pp. 221 ff.