Author: larry

My geometry animations cleared 100K views and are closing in on 110K! Half of those views are from the insanely popular Root Spiral of Theodorus:

And about a sixth of the 100,000 + views are from its companion video, Constructing Square Roots on the Number Line:

As always, you can download the PowerPoint slideshows these animations were made from by clicking on the Animations tab. That way, you can modify them and pace them to suit your students and your style.

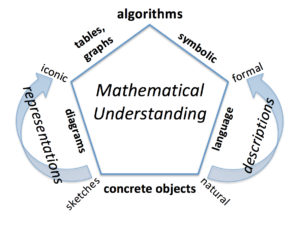Here’s a new adaptation I just finished making of Richard Lesh’s translation model. (Google something like “Richard Lesh translation model” and you should have plenty to look at, including an adaptation I put together in MS Word about 10 years ago—(which you once could have found at www.soesd.k12.or.us/math, but that link is now dead.) The source I used for Lesh’s original model was Kathleen Cramer’s “Using a Translation Model for Curriculum Development and Classroom Instruction”, which appeared in a book edited by Lesh himself (2003).

I departed from Lesh’s model for a variety of reasons. I think that understanding any given thing in mathematics—whether you’re understanding it yourself, explaining it to other people, or checking to see if they understand whatever it was—is built up through an interaction of a lot of different things. If students can’t build up a concept explicitly from these various aspects but can only fall back on rote-learning or some mystical grok-it-and-rock-it incantations, it ain’t understanding: it’s a sign that they don’t understand a concept well enough to learn the next thing and may very well not be able even to remember the original jingles well enough later on to solve the problems they were made for.

I wanted algorithms sitting at the top because I believe algorithms represent great human achievements and serve us as compact “knowledge packets” (to use Liping Ma’s great phrase), which, if we actually understand what’s going on in the workings of algorithm and are not just going through the motions, can readily serve as the solid foundation for the next step in our knowledge of math.

At the base we’ve got concrete objects to work with. This is typical in early grades; later on we may tell students something I heard Hung-Hsi Wu say many times in his lectures, “Let’s try some numbers”, treating specific numbers as if they were concrete objects we could experiment on mathematically.

As the model shows, we can record what we’ve done or what we are doing by making sketches (the representations arrow going up and around the left side). We can describe what we’re up to (the descriptions arrow going up and around the right side) in natural language, i.e., everyday speech, but as our understanding advances, we need to formalize our descriptions with definitions and conventions. As we progress, representations and descriptions get more formal and iconic, leading us through tables and graphs and through symbolic expressions to an algorithm which becomes our standard operating procedure for addressing the problems that arise with this concept.

Students who are only able to do the algorithm necessary to get a correct answer, but, if questioned, can’t explain what’s they did or why, clearly don’t have a complete picture. It’s as if the pentagon and their understanding got flattened to a line segment underlining the word “algorithm”. I would suspect students showing this behavior had been trained to a degree of perfection in some little dance without meaning, maybe even accompanied by a catchy jingle, but I would expect most of them would have trouble with more advanced topics that always follow.

My solution to this—I hope you’ve guessed by now—would not be more jingles: garbled jingles are a rich source of students’ errors, especially in high school, when they may thrash cluelessly, vainly trying to remember how the catchy jingle went so they can get an answer.

When I checked the youtube stats this morning I saw that Root Spiral of Theodorus, my most popular animation, had 30,003 views—a palindrome, as a little frosting on the cake!

The total number of views for all my videos is over 65,000 now. Currently nearly 80% of the viewers are from India, while a little over 10% of the views are from the USA.

Just passed 50K total views worldwide on my math video animations channel! Root Spiral of Theodorus is the most popular with over 18K views. Leading countries (currently) are India (53%), USA (18%), and UAE (13%).

Until a few years ago, I didn’t know Theodorus from brontosaurus. But then, somehow, I heard about it, and thought it could be a simple and beautiful way for kids (and other people) to start to get the hang of square roots as length.

I thought I could probably do an animation of it in PowerPoint. I did, and after a bit of fussing, Root Spiral of Theodorus was the result.

It’s been quite popular: over 18,000 views since I uploaded it last April. If you google “root spiral of theodorus”, it comes up #2 out of 26,300 results, right after Wikipedia.

If you like this one enough to use with your students, as with all my other animations, you can download the PowerPoint file from my “Animations” folder and have a version you can teach with, turning off the timed settings and advancing it slide by slide to suit your purposes, or even modify the content to according to your whim or needs. I’d like to get credit, naturally, but if you’d prefer simply stealing it, oh well….

My YouTube channel, youtube.com/user/bikes4fish, just passed 35,000 views!

“Root Spiral of Theodorus” has been the most popular lately—over 7500 views in the 9 months since I posted it. But the most popular overall in total views is still “Composition of Rigid Motions (translation, rotation, and reflection)” with nearly 14,000 views since I posted it 3 years ago.

I got an early start this morning and posted Power Point .pptx slide shows for each of my 6 youtube video animations—the 3 basic rigid motions ones and the 3 Pythagorean Theorem ones. I put them in Animations so interested people could download the slide shows in pptx form and modify to their hearts’ content. If you want to use any of them for teaching, you could make some changes in Power Point: un-select the “Use Timings” box if it’s selected, and for a lot of the animations, change the Animations Options from “Start: After Previous” to “Start: On Click”. This will enable you to “drive” the presentation yourself, advancing the slides and animations to suit the pacing of your lesson with your students. Of course, it will also enable you to change things to suit your own aesthetic sensibilities. Go crazy.