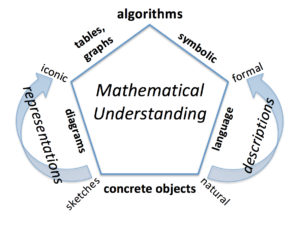
 Here’s a new adaptation I just finished making of Richard Lesh’s translation model. (Google something like “Richard Lesh translation model” and you should have plenty to look at, including an adaptation I put together in MS Word about 10 years ago—(which you once could have found at www.soesd.k12.or.us/math, but that link is now dead.) The source I used for Lesh’s original model was Kathleen Cramer’s “Using a Translation Model for Curriculum Development and Classroom Instruction”, which appeared in a book edited by Lesh himself (2003).
Here’s a new adaptation I just finished making of Richard Lesh’s translation model. (Google something like “Richard Lesh translation model” and you should have plenty to look at, including an adaptation I put together in MS Word about 10 years ago—(which you once could have found at www.soesd.k12.or.us/math, but that link is now dead.) The source I used for Lesh’s original model was Kathleen Cramer’s “Using a Translation Model for Curriculum Development and Classroom Instruction”, which appeared in a book edited by Lesh himself (2003).
I departed from Lesh’s model for a variety of reasons. I think that understanding any given thing in mathematics—whether you’re understanding it yourself, explaining it to other people, or checking to see if they understand whatever it was—is built up through an interaction of a lot of different things. If students can’t build up a concept explicitly from these various aspects but can only fall back on rote-learning or some mystical grok-it-and-rock-it incantations, it ain’t understanding: it’s a sign that they don’t understand a concept well enough to learn the next thing and may very well not be able even to remember the original jingles well enough later on to solve the problems they were made for.
I wanted algorithms sitting at the top because I believe algorithms represent great human achievements and serve us as compact “knowledge packets” (to use Liping Ma’s great phrase), which, if we actually understand what’s going on in the workings of algorithm and are not just going through the motions, can readily serve as the solid foundation for the next step in our knowledge of math.
At the base we’ve got concrete objects to work with. This is typical in early grades; later on we may tell students something I heard Hung-Hsi Wu say many times in his lectures, “Let’s try some numbers”, treating specific numbers as if they were concrete objects we could experiment on mathematically.
As the model shows, we can record what we’ve done or what we are doing by making sketches (the representations arrow going up and around the left side). We can describe what we’re up to (the descriptions arrow going up and around the right side) in natural language, i.e., everyday speech, but as our understanding advances, we need to formalize our descriptions with definitions and conventions. As we progress, representations and descriptions get more formal and iconic, leading us through tables and graphs and through symbolic expressions to an algorithm which becomes our standard operating procedure for addressing the problems that arise with this concept.
Students who are only able to do the algorithm necessary to get a correct answer, but, if questioned, can’t explain what’s they did or why, clearly don’t have a complete picture. It’s as if the pentagon and their understanding got flattened to a line segment underlining the word “algorithm”. I would suspect students showing this behavior had been trained to a degree of perfection in some little dance without meaning, maybe even accompanied by a catchy jingle, but I would expect most of them would have trouble with more advanced topics that always follow.
My solution to this—I hope you’ve guessed by now—would not be more jingles: garbled jingles are a rich source of students’ errors, especially in high school, when they may thrash cluelessly, vainly trying to remember how the catchy jingle went so they can get an answer.